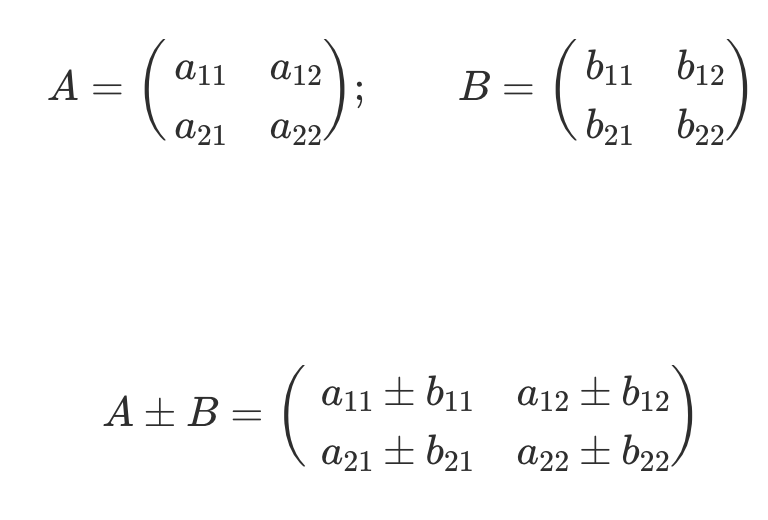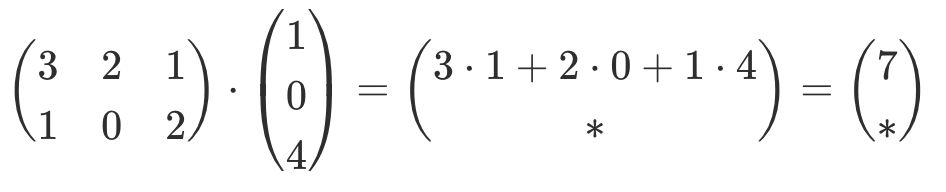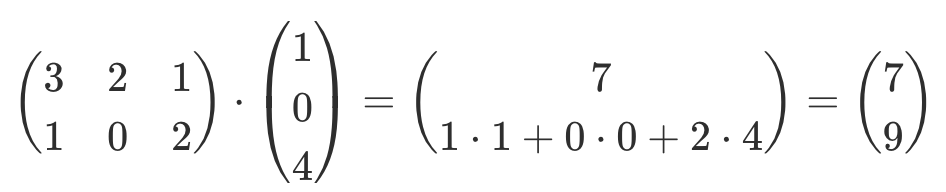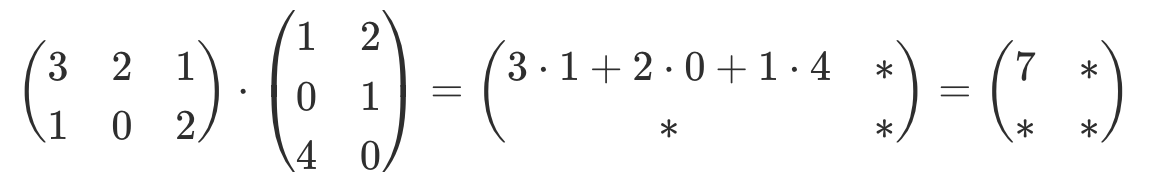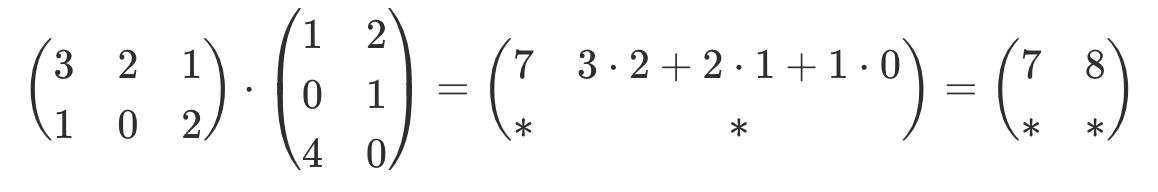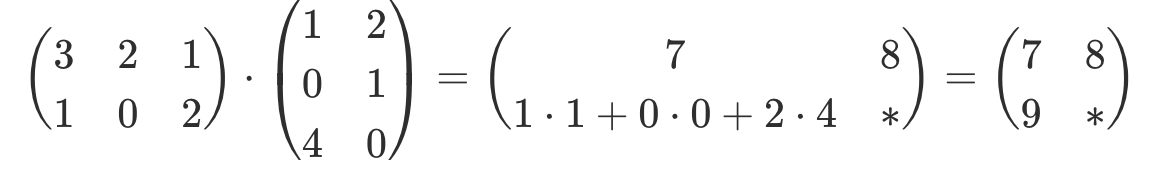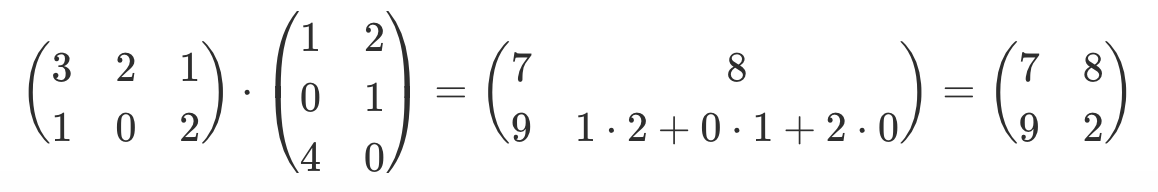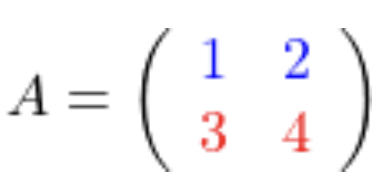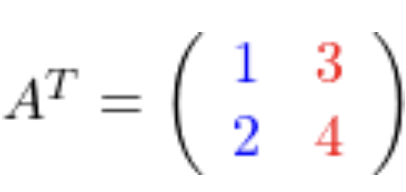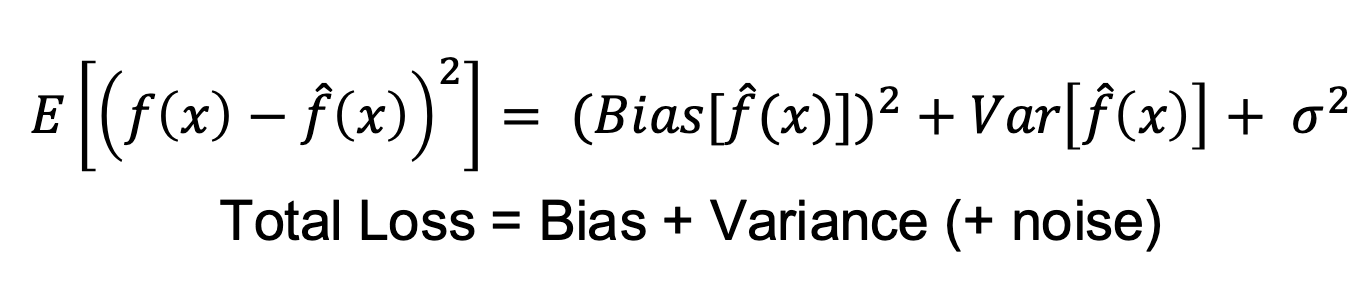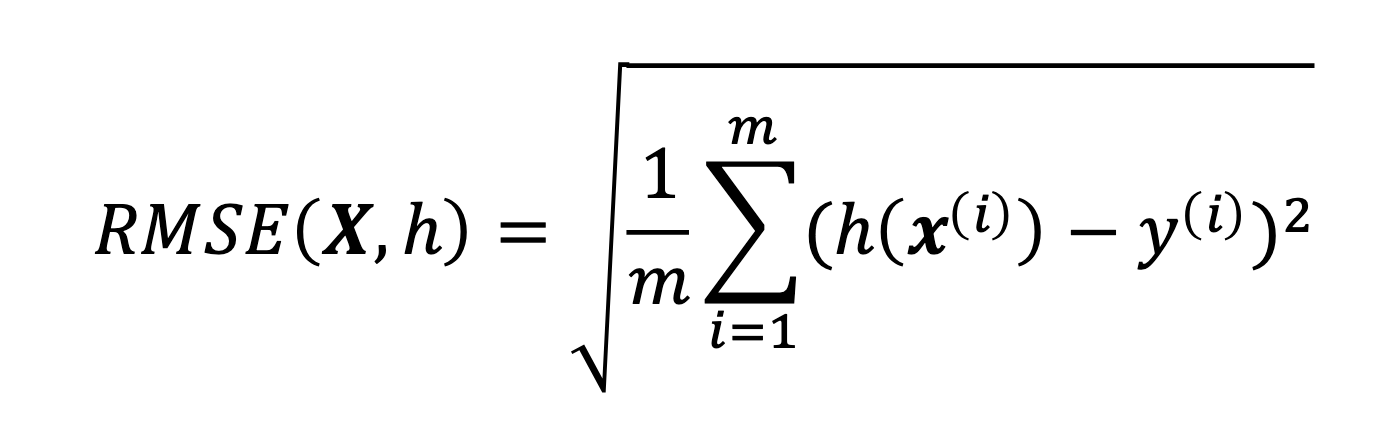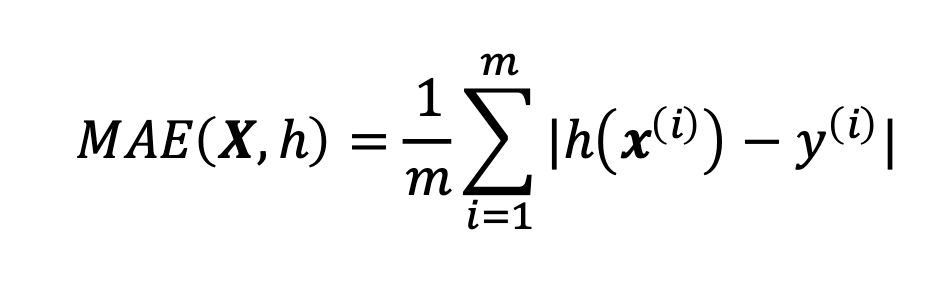cds1011/zusammenfassung/zusammenfassung.md

Zusammenfassung für CDS-1011 Einführung in Data Science

Grundbegriffe

Begriff	Beschreibung
Daten	Beispiele: Transaktionsdaten, Log-Daten, Maschinendaten, Dokumente / Texte, Social Media, Videos, Bilder
Data Science	Fachgebiet, welches sich mit der Gewinnung von Wissen aus Daten beschäftigt
Artificial Intelligence	Systeme, die intelligentes Verhalten aufweisen. Indem sie ihre Umgebung analysieren und Massnahmen ergreiffen, mit einen gewissen Grad an Selbstbestimmung. Um dann bestimmte Ziele zu erreichen
Machine Learning	Machine Learning beschäftigt sich mit der Frage, wie man Computer Programme so entwerfen kann, dass sie sich, mit Erfahrung, automatisch verbessern
Deep Learning	Deep Learning ist eine unterkategorie von AI, die ihren Fokus auf die Erstellung von künstlichen neuronalen Netzen (KNN) setzt. KNN sind in der Lage, genaue datengestützte Entscheidungen zu treffen
Features	Features sind die verschiedenen Attribute, die einen informationsreichen Datensatz bilden, der zum Trainieren von Modellen für maschinelles Lernen verwendet wird. Diese Merkmale werden als Eingabe für das Modell verwendet, um genaue Vorhersagen für die Labels zu treffen.
Labels (Zielvariablen)	Ein Label, auch als Zielvariable oder abhängige Variable bezeichnet, ist die Ausgabe, für deren Vorhersage das Modell trainiert wird. Beim überwachten Lernen sind Labels die bekannten Ergebnisse, die das Modell während des Trainings mit den Eingabemerkmalen zu verknüpfen lernt.
Parameter	Ein Parameter ist eine Variable, die während des Trainingsprozesses aus den Daten gelernt wird. Er wird verwendet, um die zugrunde liegenden Beziehungen in den Daten darzustellen und um Vorhersagen über neue Daten zu treffen.
Hyperparameter	A hyperparameter, on the other hand, is a variable that is set before the training process begins. It controls the behaviour of the learning algorithm, such as the learning rate, the regularization strength, and the number of hidden layers in a neural network. Z.B. Anzahl Clusters bei einer Clustering Aufgabe

Machine Larning

Begriff	Beschreibung
Überwachtes Lernen	Überwchtes Lernen nutzt Beispieldaten mit einer Zielvariable, um aus diesen Daten Muster zu erlernen und diese auf unbekannte Daten anzuwenden Wird für Klassifikationen und Regressionen genutzt, also für die Vorhersage von Wahrscheinlichkeiten oder numerischen Werten Überwachtes Lernen setzt eine aufwendige Datenvorverarbeitung voraus
Klassifizierung	Methode des überwachten Lernens, bei der ein Modell anhand von gelabelten Beispieldaten lernt, neue Datenpunkte vordefinierten Kategorien (Klassen) zuzuordnen, z.B. Bilder als "Hund" oder "Katze" zu erkennen, Spam-Mails zu filtern oder Kunden abzuwandern
Klassifizierung Algorithmen	K-Nearest-Neighbors Naïve Bayes Support Vector Machines Decision Trees
Lineare Regression	Ziel: Vorhersage des Werts einer stetigen Variable Output: Reele Zahl Beispiel: Wie hoch ist der Schlusskurs einer Aktie morgen?
Logistische Regression	Ziel: Vorhersage, ob ein bestimmtes kategoriales Ergebnis eintritt (binär, multinomial, ordinal) Output: Wahrscheinlichkeit, die dann in eine Klasse übersetzt wird Beispiel: Wird die Aktie morgen mindestens den Kurs n erreichen? (Ja = 1, Nein = 0)
Modell	Ein Machine-Learning-Modell ist ein Programm, das Muster findet oder auf Basis eines zuvor ungesehenen Datasets Entscheidungen trifft.
Unüberwachtes Lernen	Unüberwachtes Lernen (Unsupervised Learning) ist ein Bereich des maschinellen Lernens, bei dem Algorithmen Muster und Strukturen in ungelabelten Daten selbstständig entdecken, ohne vorherige menschliche Anleitungen oder vordefinierte Zielwerte.
Halbüberwachtes Lernen	Beim Semi-Supervised Learning wird ein Modell sowohl mit beschrifteten als auch mit unbeschrifteten Daten trainiert. Dabei lernt der Algorithmus mithilfe weniger gelabelter Datenpunkte, Muster in den Dateninstanzen ohne bekannte Zielvariable zu erkennen, was zu einer präziseren und effizienteren Modellbildung führt.
Reinforcement Learning	Reinforcement Learning ist ein Teilgebiet des maschinellen Lernens, das sich darauf konzentriert, wie Agenten durch Trial and Error lernen können, Entscheidungen zu treffen, um die kumulativen Belohnungen zu maximieren. RL ermöglicht es Maschinen, durch Interaktion mit einer Umgebung und durch Feedback zu ihren Handlungen zu lernen. Dieses Feedback erfolgt in Form von Belohnungen oder Strafen.
Batch Learning	Beim Batch-Lernen, auch Offline-Lernen genannt, wird ein maschinelles Lernmodell auf den gesamten Datensatz gleichzeitig trainiert, was zu einem statischen Modell führt, das nicht aus neuen Daten in der Produktion lernt und regelmässig mit aktualisierten Daten neu trainiert werden muss, um effektiv zu bleiben.
Online Learning	In der Informatik ist Online-Maschinelles Lernen eine Methode des maschinellen Lernens, bei der Daten in sequenzieller Reihenfolge verfügbar werden und dazu verwendet werden, bei jedem Schritt den besten Prädiktor für zukünftige Daten zu aktualisieren. Dies steht im Gegensatz zu Batch-Lernverfahren, bei denen der beste Prädiktor durch das gleichzeitige Lernen anhand des gesamten Trainingsdatensatzes generiert wird.
Instanzbasiertes Lernen	Eine einfache Methode besteht darin, dass das System direkt die Merkmale von neuen Datenpunkten mit denen der gelernten Datenpunkte vergleicht und ihre Ähnlichkeit vergleicht. Das bezeichnet man als instanzbasiertes Lernen. In der Trainingsphase lernt das System nur die Trainingsdaten.

Matrizen Operationen	Beispiel
Addition
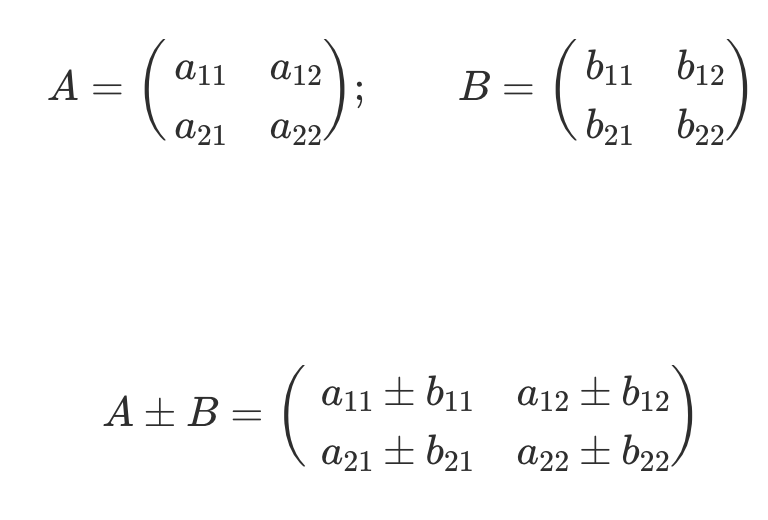Multiplikation mit Vektor
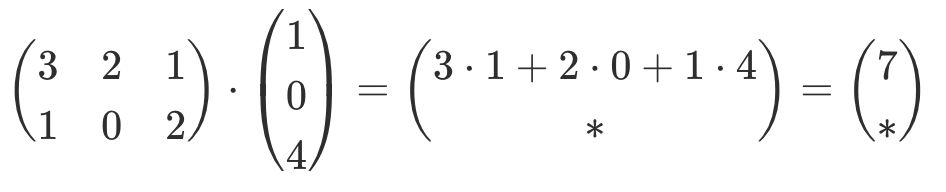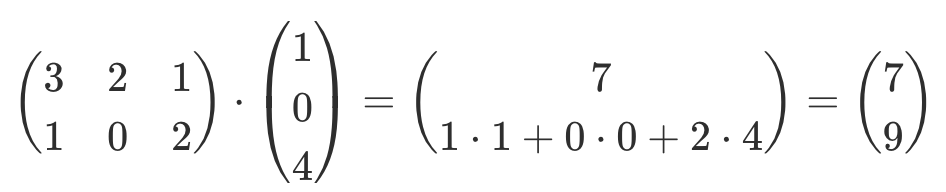Multiplikation
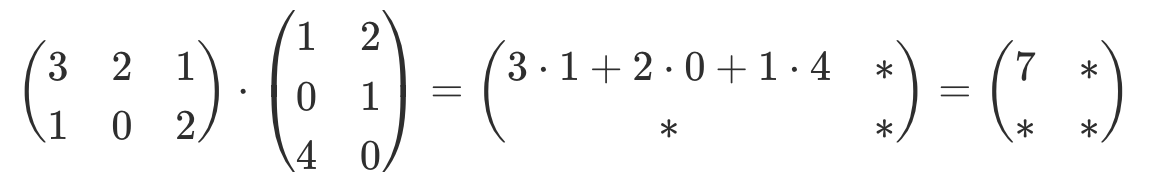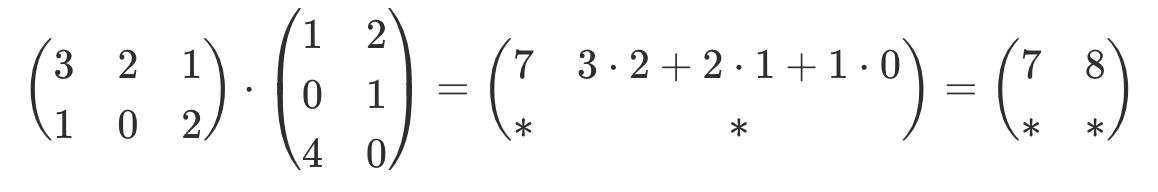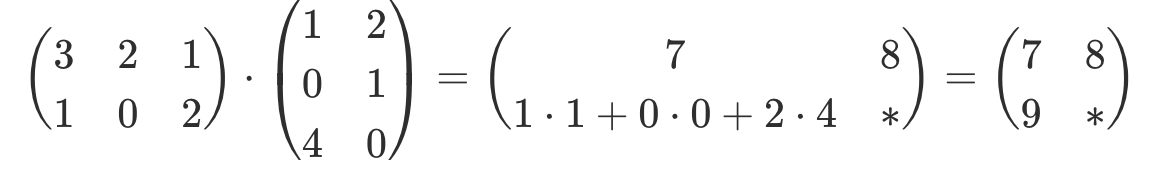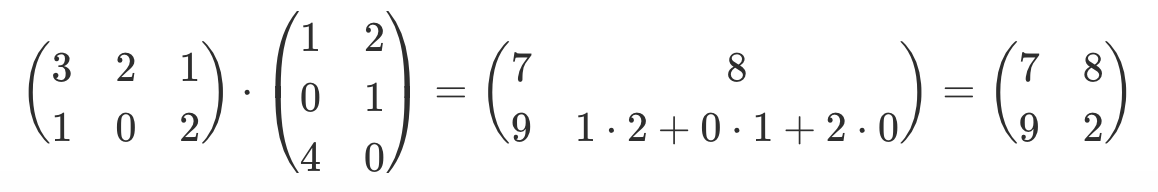Transponierte Matrizen

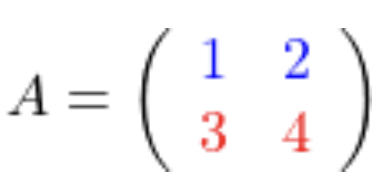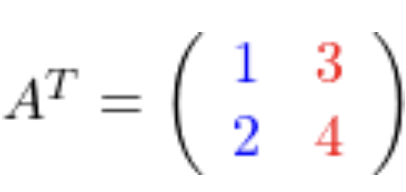Herausforderungen

Begriff	Beschreibung
Bias	Fehler, der entsteht, weil das Modell das Konzept nicht abbilden kann
Sampling Bias	Bestimmte Gruppen unterreoräsentiert
Measurement Bias	Fehelr in der Erhebung (z.B. Sensoren)
Survivor Bias	Nur erfolgreiche Fälle in den Daten
Confirmation Bias	Bewusste/unterbewusste Selektion von Daten
Data Cleaning & Wrangling	Ausreisser entfernen Fehler beheben Lückenhafte Merkmale (ignorieren, entfernen, ergänzen)
Varianz	Fehler, der entsteht, weil der Lernalgorithmus überempfindlich auf kleine Änderungen in den Trainingsdaten reagiert. Gesamtfehler eines Modells wird durch die Summe von Bias-Quadrat, Varianz und Rauschen ausgedrückt: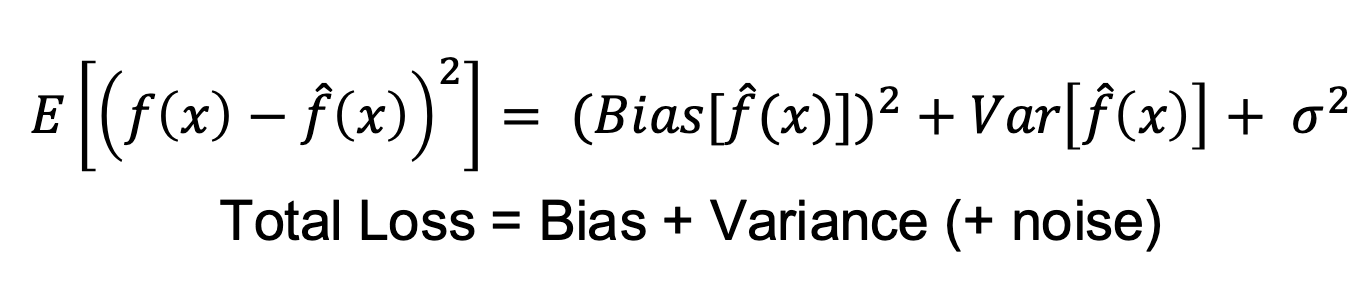
Underfitting	Modell ist zu einfach, um die in den Daten enthaltene Struktur zu erlernen. Möglichkeiten um Underfitting zu beheben: Mächtigeres Modell, Feature Selection, Hyperparameter
Overfitting	Modell passt sich gut auf die Trainingsdaten an, kann aber nicht Verallgemeinern. Möglichkeiten um Overfitting zu beheben: Modell vereinfachen, Anzahl Features reduzieren, Umfang der Traingsdaten erhöhen, Rauschen reduzieren, Regularisierung (Restriktionen Hyperparameter)
Irrelevante Features	Welche Merkmale sind relevant fürs Modell
Data Snooping	Data Snooping ist eine Form der statistischen Verzerrung, bei der Daten oder Analysen manipuliert werden, um künstlich statistisch signifikante Ergebnisse zu erzielen.
Cross Validation	Cross Validation ist eine Technik, mit der überprüft wird, wie gut ein maschinelles Lernmodell bei unbekannten Daten funktioniert, während gleichzeitig Overfitting verhindert wird. Dabei wird wie folgt vorgegangen: Der Datensatz wird in mehrere Teile aufgeteilt. Das Modell wird an einigen Teilen trainiert und an den übrigen Teilen getestet. Dieser Resampling-Prozess wird mehrfach wiederholt, wobei jeweils unterschiedliche Teile des Datensatzes ausgewählt werden. Die Ergebnisse jedes Validierungsschritts werden gemittelt, um die endgültige Leistung zu ermitteln.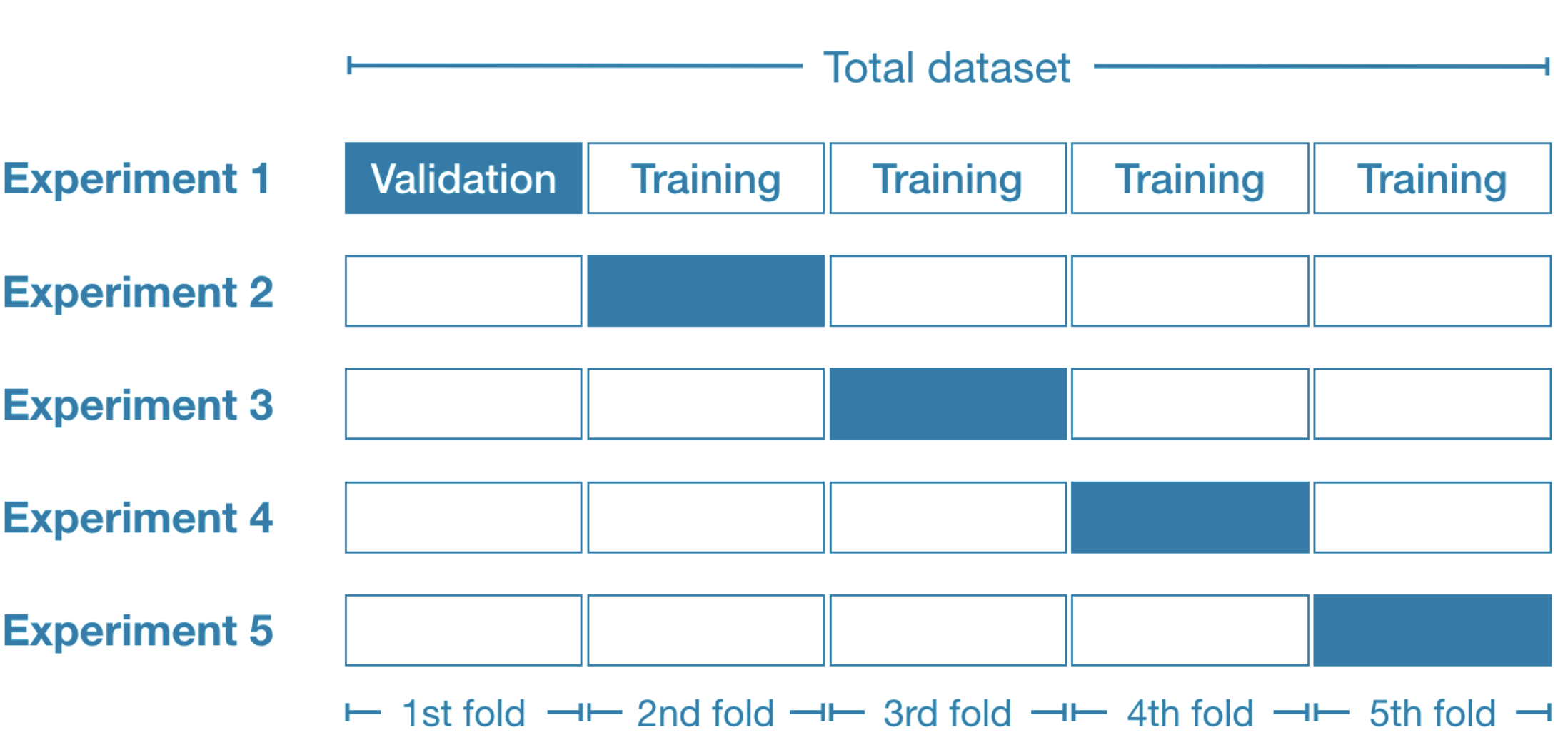

Explorative Datenanalyse

Begriff	Beschreibung
Explorative Datenanalyse	Explorative Datenanalyse (EDA) bezeichnet den Prozess, bei dem Daten untersucht, visualisiert und beschrieben werden, um erste Einsichten zu gewinnen, Zusammenhänge zu erkennen und Hypothesen zu formulieren — noch bevor Modellierung oder Hypothesentestsstattfinden.
Mittlere quadratische Abweichung (RMSE)	m ist die Anzahl Datenpunkte im Datensatz h ist die Vorhersagefunktion des Systems X ist die Matrix mit den Werten sämtlicher Merkmale x(i) Vektor der Werte aller Merkmale y(i) Label (gewünschter Ausgabewert)
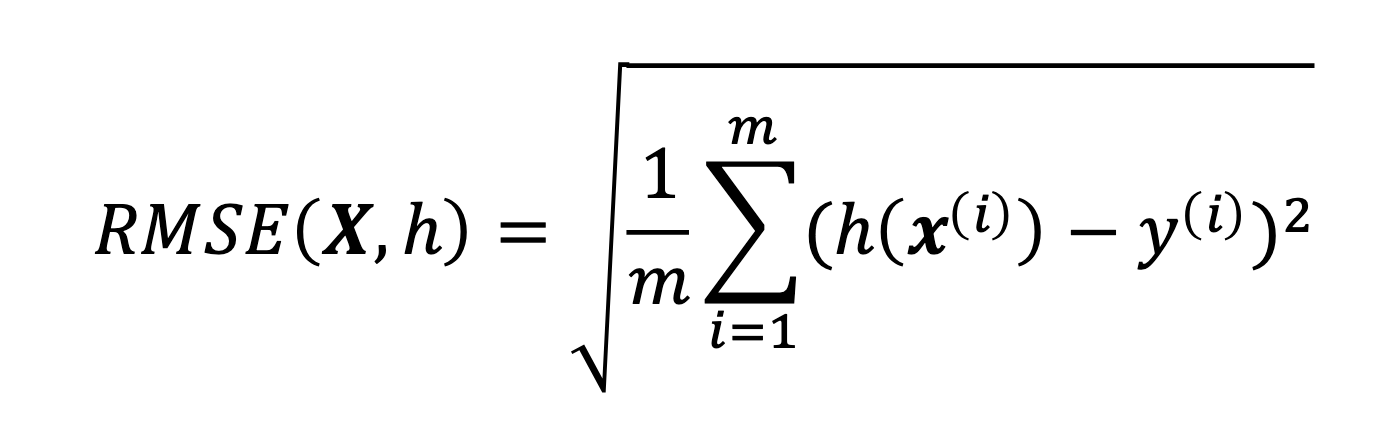Mittlerer absoluter Fehler (MAE)	m ist die Anzahl Datenpunkte im Datensatz h ist die Vorhersagefunktion des Systems X ist die Matrix mit den Werten sämtlicher Merkmale x(i) Vektor der Werte aller Merkmale y(i) Label (gewünschter Ausgabewert)
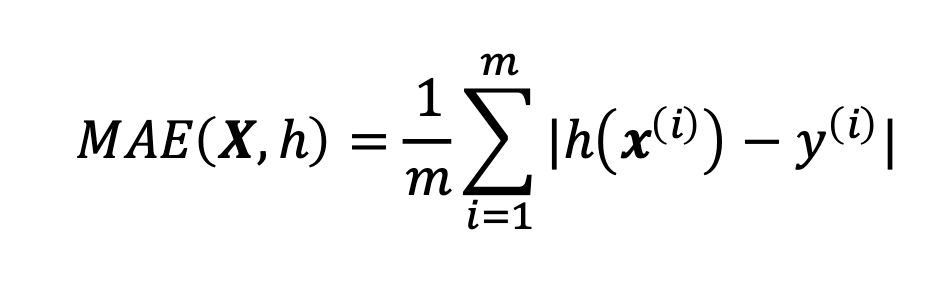Stetige Merkmale	Belibigen Wert innerhalb eines Intervalls Unendlich viele Ausprägungen Beispiele Strekenlänge Zeitintervalle Gewicht
Diskrete Merkmale	Endliche Anzahl Ausprägungen Menge ist zählbar Beispiele Schulnoten Haarfarben Geschlechter Anzahl Teilnehmer eines Sportanlasses
Skalenniveaus
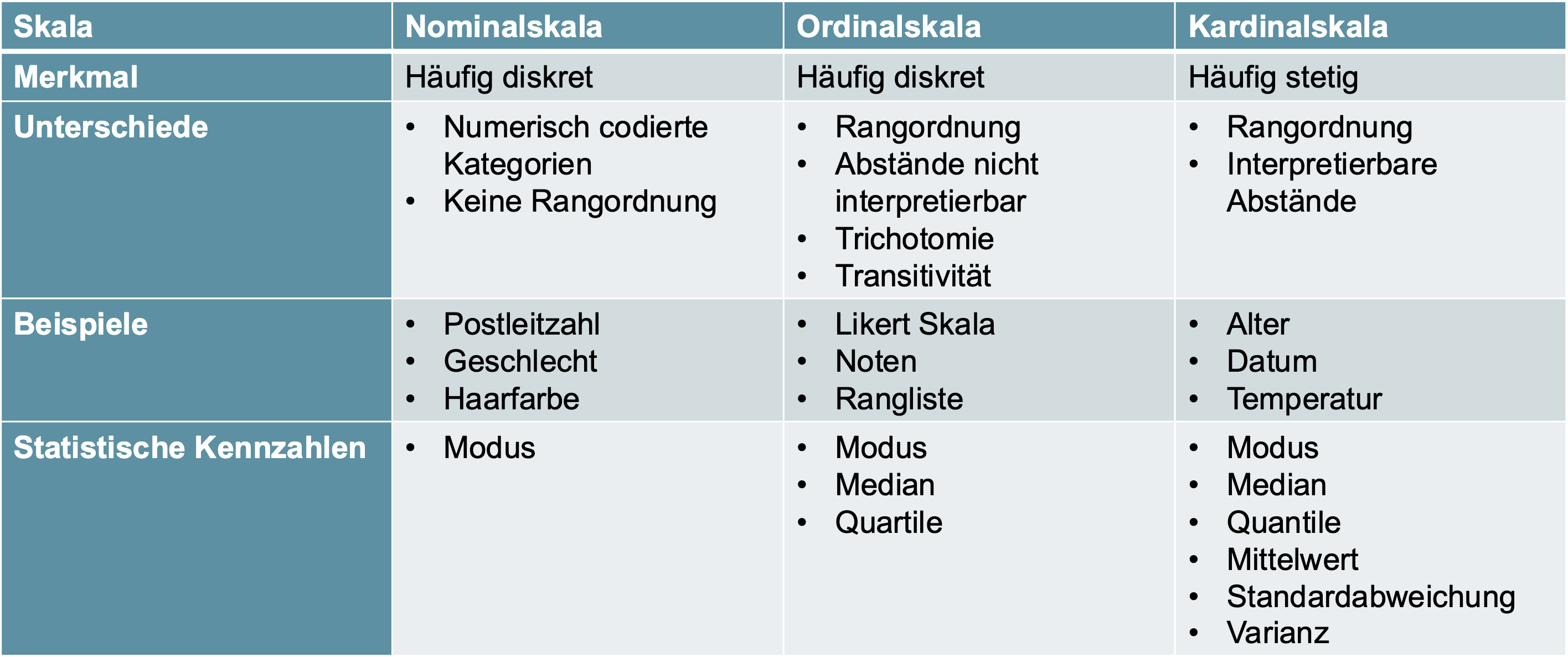Mittelwert	Summe aller Werte dividiert durch die Anzahl von Werten. \huge \bar{x} = \frac{\sum_{i=1}^{n} x_i}{n}
Median	Mittlerer Wert der sortierten Liste. \\ \huge \text{Median} = \tilde{x} = \begin{cases}x_{\left(\frac{n+1}{2}\right)}, & \text{wenn } n \text{ ungerade ist} \\ \\ \frac{x_{\left(\frac{n}{2}\right)} + x_{\left(\frac{n}{2}+1\right)}}{2}, & \text{wenn } n \text{ gerade ist}\end{cases}
Varianz	\huge Varianz = s^2 = \frac{\sum_{i=1}^{n} (x_i - \bar{x})^2 }{n - 1}
Standardabweichung	\huge Standardabbwichung = s = \sqrt{Varianz}
Mittlere Absolute Abweichung	\huge \text{Mittlere Absolute Abweichung} = \frac{\sum_{i=1}^{n} \lvert x_i - \bar{x} \rvert}{n - 1}
Pearson Korrelationskoeffizient	Zusammenhang zwischen zwei numerischen Variablen. \huge r = \frac{\sum_{i=1}^{n} (x_i - \bar{x})(y_i - \bar{y})}{(n - 1)\, s_x s_y} r \in [-1;1] 1 stark positive Korrelation 0 keine Korrelation -1 stark negative Korrelation

Lineare Regression

Begriff	Beschreibung
Feature Engineering	Struktur des Konzept des ML Modell visualisieren Auswahl der Features für das ML Modell Trifft nicht auf Deep Learning zu
Regressionsgerade	Summe der quadrierten Abstände der einzelnen Messpunkte zur Geraden minimal.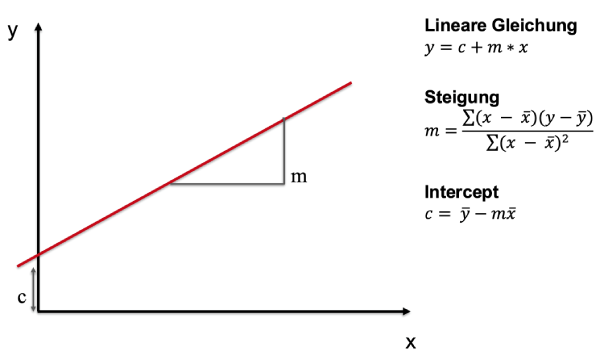

Regressionsgerade berechnen

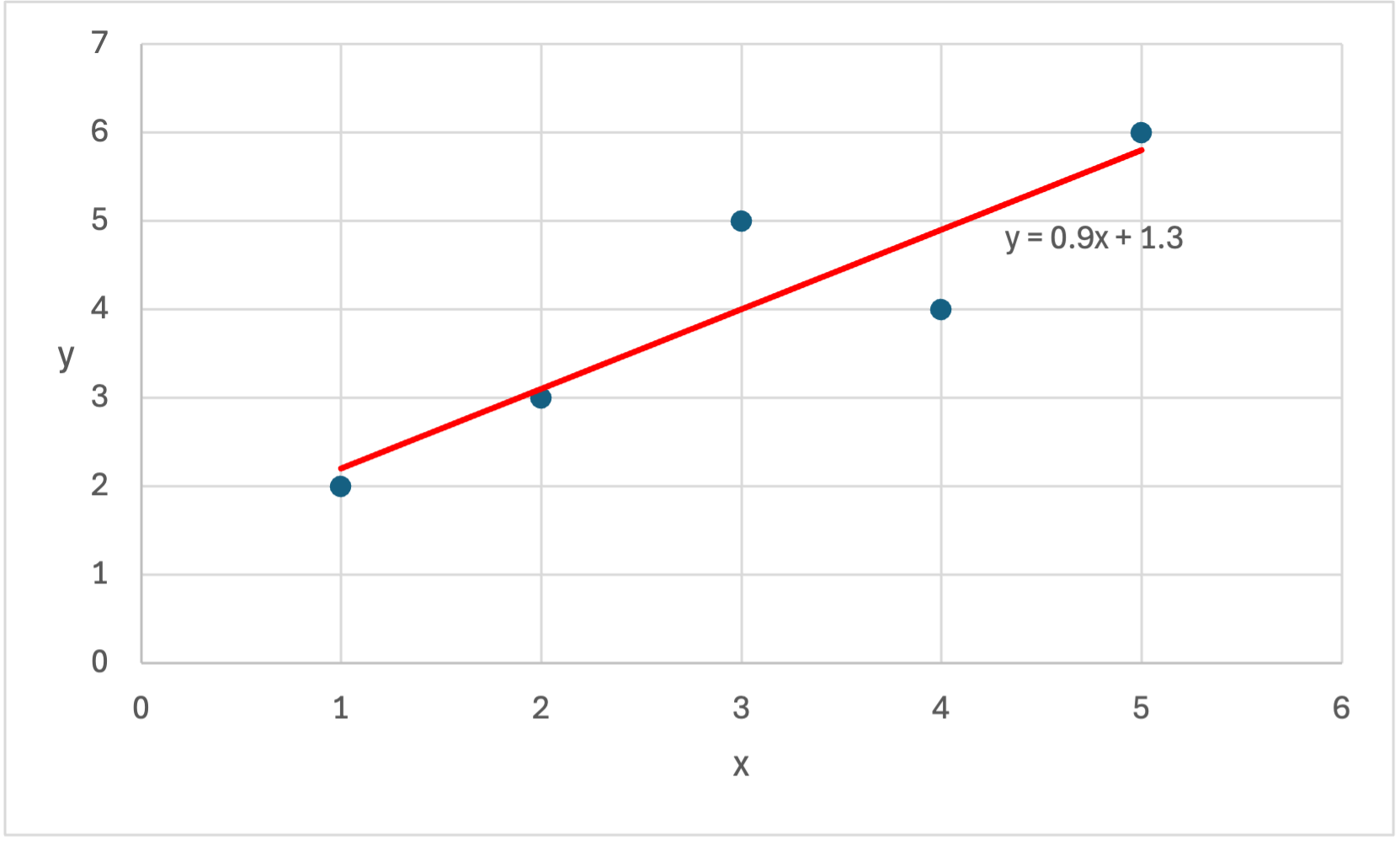
Beispiel:

x = [1, 2, 3, 4, 5], y = [2, 3, 5, 4, 6] \\

1. x, y Tabelle erstellen

	x	y	x*y	x2
	1	2	2	1
	2	3	6	4
	3	5	15	9
	4	4	16	16
	5	6	30	25
\sum	15	20	69	55

2. c Wert berechnen

c = \frac{\sum_y * \sum_x - \sum_x * \sum_{xy}}{n(\sum_{x^2}) - (\sum_x)^2} \\[1em]

c = \frac{20 * 55 - 15 * 69}{5*55 - 15^2} = 1.3

3. m Wert berechnen

m = \frac{n(\sum_{xy}) - \sum_x * \sum_y}{n(\sum_{x^2} - (\sum_x)^2)} \\[1em]

m = \frac{5 * 69 - 15 * 20}{5 * 55 - 15^2} = 0.9

4. Werte in Formel einsetzen

\hat{y} = mx+c \\
\hat{y} = 0.9x+1.3

5. Funktionsgraphen mit Regressionsgerade Zeichnen

Kennzahlen der Regressionsanalyse R²

Begriff	Beschreibung
R2	Wie gut kann die abhängige Variable durch die unabhängige Variable vorhergesagt werden?
SSR	Sum of squares regression. Welcher Varianzanteil des Kriteriums kann mithilfe der Prädikatoren erklärt werden?
SST	Sum of squares total. Werte zwischen 0 und 1. Je höher der Wert, desto genauer die Vorhersage
yi	Abhängige Variable
\tilde{y}	Median der abhängigen Variable
\hat{y}	Vorhergesagte abhängige Varbiable

Beispiel:

x = [1, 2, 3, 4, 5], y = [2, 3, 5, 4, 6]

\hat{y} = 0.9x+1.3

\hat{y} = [2.2, 3.1, 4, 4.9, 5.8]

1. Median von y finden

y = [2, 3, 5, 4, 6] sortieren \rightarrow y = [2, 3, 4, 5, 6]

i_{\tilde{y}} = \frac{5+1}{2} = 3 

\tilde{y} = y[i_{\tilde{y}}] = 4

2. SST berechnen

SST = \sum_{i=1}^{n} (y_i-\tilde{y})^2

SST = (2-4)^2+(3-4)^2+(5-4)^2+(4-4)^2+(6-4)^2 = 10

3. SSR berechnen

SSR = \sum_{i=1}^{n} \hat{y}_i-\tilde{y})^2

SSR = (2.2-4)^2+(3.1-4)^2+(4-4)^2+(4.9-4)^2+(5.8-4)^2 = 8.1

4. R2 berechnen

R^2 = \frac{SSR}{SST}

R^2 = \frac{8.1}{10} = 0.81

5. Interpretieren 0.81 bedeutet, dass viele der Datenpunkte in der Nähe der Regressionsgerade sind

Klassifikation

Unsupervised Learning Clustering